Black-body-Radiation

This project illustrates one of the most important problems in the history of physics:

The Ultraviolet Catastrophe: Classical physics (Rayleigh-Jeans) predicted infinite energy at short wavelengths
The Birth of Quantum Mechanics: Planck’s solution required assuming energy quantization (E = hν)

Overview

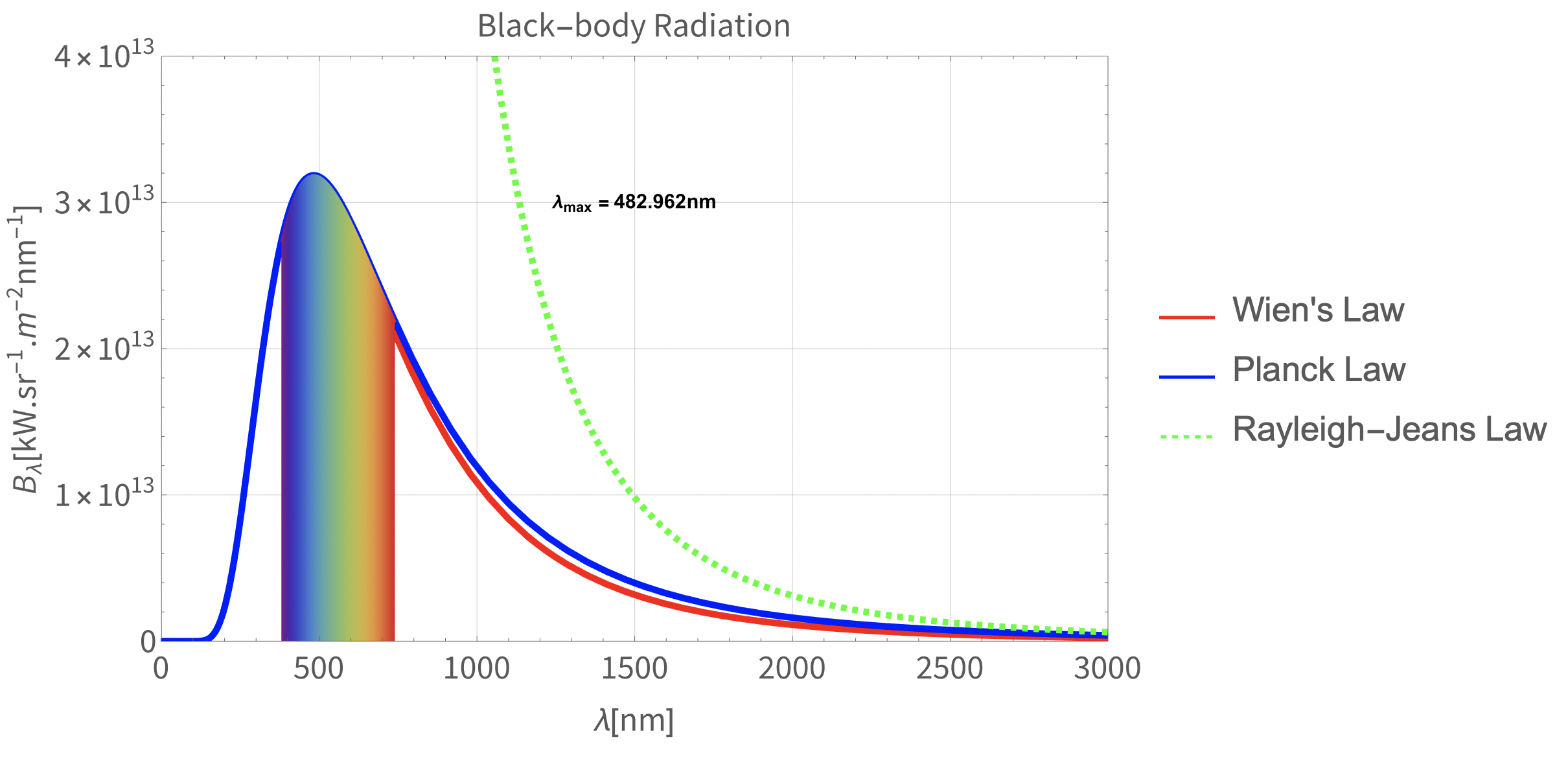
Blackbody radiation describes the electromagnetic radiation emitted by an idealized object that absorbs all incident radiation. This project illustrates three fundamental laws that attempt to describe the spectral radiance of blackbody radiation:

Rayleigh - Jeans Law

The classical approach based on equipartition theorem and wave theory. This law accurately describes long-wavelength (low-frequency) radiation but fails at short wavelengths, leading to the “ultraviolet catastrophe” where it predicts infinite energy.

$https://latex.codecogs.com/svg.image?\text{B}(\lambda)\text{:=}\frac{2 c k T}{\lambda ^4}$

Where:

B(λ) = spectral radiance
c = speed of light
k = Boltzmann constant
T = absolute temperature
λ = wavelength

Planck’s Law

The complete quantum mechanical solution that revolutionized physics. Introduced by Max Planck in 1900, this law correctly describes blackbody radiation at all wavelengths by treating electromagnetic energy as quantized. It resolves the ultraviolet catastrophe and reduces to both the Rayleigh-Jeans law at long wavelengths and Wien’s approximation at short wavelengths.

$https://latex.codecogs.com/svg.image?\text{B}(\lambda )\text{:=}\frac{2 hc^2 }{\lambda ^5 \left(\exp \left(\frac{hc}{\lambda k T}\right)-1\right)}$

Where:

h = Planck constant
c = speed of light
k = Boltzmann constant
T = absolute temperature
λ = wavelength

Wien’s Approximation

A semi-empirical formula proposed by Wilhelm Wien in 1896 that accurately describes short-wavelength (high-frequency) radiation. This approximation is valid when h c / (λ k T) » 1, making it useful for UV and higher energy radiation. It predates Planck’s law and was an important step toward the quantum theory.

$https://latex.codecogs.com/svg.image? \text{B}(\lambda )\text{:=}\frac{\left(2hc^2 \right) \exp \left(-\frac{hc}{\lambda k T}\right)}{\lambda ^5}$

Where:

h = Planck constant
c = speed of light
k = Boltzmann constant
T = absolute temperature
λ = wavelength

Visualization

The plot below compares all three laws across different wavelengths, clearly showing:

How Rayleigh-Jeans law diverges at short wavelengths (UV catastrophe)
How Wien’s approximation matches Planck’s law at short wavelengths
How Rayleigh-Jeans matches Planck’s law at long wavelengths
The complete accuracy of Planck’s law across the entire spectrum

BBR

Licence

Released under licence: the GPL version 3 license.

Using without reference is, among other things, against the current license agreement (GPL).

Scientific or technical publications resulting from projects using this code are required to citate.